QCM-CONCOURS-GRATUITS: Maths cat :C

Affichage des articles dont le libellé est Maths cat :C. Afficher tous les articles

Exercices de mathématique pour préparer le CAP cuisine

Question : Si 1 kg de pommes de terre coûte 1,20 €, combien coûte 3,5 kg de pommes de terre ?
Correction : Le coût d'un kilogramme de pommes de terre est de 1,20 €. Pour connaître le coût de 3,5 kg, il faut multiplier 1,20 € par 3,5. Le coût de 3,5 kg de pommes de terre est donc de 4,20 €.
Question : Une cantine achète des carottes à 0,70 € le kg. Si elle achète 25 kg de carottes, combien va-t-elle payer ?
Correction : Le coût d'un kilogramme de carottes est de 0,70 €. Pour connaître le coût de 25 kg de carottes, il faut multiplier 0,70 € par 25. La cantine va donc payer 17,50 €.
Question : Une recette de pâte à pizza nécessite 500 g de farine. Si une cantinière doit préparer 10 pizzas, combien de farine va-t-elle utiliser ?
Correction : Une pizza nécessite 500 g de farine, donc 10 pizzas nécessitent 10 x 500 = 5000 g (ou 5 kg) de farine.
Question : Un sac de riz pèse 20 kg. Si une cantinière utilise en moyenne 125 g de riz par personne, combien de personnes peuvent être nourries avec un sac de riz ?
Correction : Un sac de riz pèse 20 kg, soit 20 000 g. En divisant 20 000 g par 125 g, on obtient que le sac de riz permet de nourrir 160 personnes.
Question : Une cantinière doit préparer une salade pour 60 personnes. La recette de la salade nécessite 200 g de tomates pour 4 personnes, 150 g de concombre pour 3 personnes et 100 g de salade pour 2 personnes. Combien de tomates, de concombres et de salade doit-elle utiliser pour préparer la salade ?
Correction : Pour 60 personnes, il faut utiliser 60/4 = 15 fois la quantité de tomates pour 4 personnes, soit 15 x 200 g = 3 kg de tomates. De même, il faut utiliser 60/3 = 20 fois la quantité de concombre pour 3 personnes, soit 20 x 150 g = 3 kg de concombre. Enfin, il faut utiliser 60/2 = 30 fois la quantité de salade pour 2 personnes, soit 30 x 100 g = 3 kg de salade.

Problèmes et exercices de mathématique niveau CAP

CAP épreuve de mathématiques tertiaires, services, hôtellerie, alimentation, restauration

Sont concernées les spécialités suivantes :

● Agent d’accueil et de conduite routière, transport de voyageurs ● Agent de prévention et de médiation ● Boucher ● Boulanger ● Bronzier : option A : monteur en bronze option B : ciseleur sur bronze option C : tourneur sur bronze ● Charcutier traiteur ● Chocolatier confiseur ● Commercialisation et services en hôtel-café-restaurant ● Conducteur livreur de marchandises ● Crémier-fromager ● Cuisine● Doreur à la feuille ornemaniste ● Émailleur d’art sur métaux ● Employé de commerce multispécialités ● Employé de vente spécialisée : option A : produits alimentaires option B : produits d’équipement courant option C : service à la clientèle option D : produits de librairie papeterie presse ● Encadreur ● Fleuriste ● Glacier fabricant ● Lapidaire option A : diamant option B : pierres de couleur ● Mareyage ● Métiers du football● Opérateur/opératrice de service – relation client et livraison ● Opérateur/opératrice logistique ● Orfèvre : option A : monteur en orfèvrerie option B : tourneur repousseur en orfèvrerie option C : polisseur aviveur en orfèvrerie option D : planeur en orfèvrerie ● Pâtissier ● Poissonnier-Écailler ● Primeur ● Taxidermiste ● Vendeur-magasinier en pièces de rechange et équipements automobiles

<<<CORRECTION>>>

Durant les vacances d’été, Thomas et Clémence se sont inscrits pour une semaine au centre de loisirs de leur commune. Plusieurs animations sont prévues en fonction de l’âge des adolescents. Exercice 1 : (4,5 points) Le premier jour, les animateurs réalisent une enquête pour connaître l’âge des adolescents inscrits. Voici tous les résultats obtenus :

Exercice 1 :

Le premier jour, les animateurs réalisent une enquête pour connaître l’âge des adolescents inscrits. Voici tous les résultats obtenus :

13 ans 12 ans 15 ans 14 ans 16 ans 14 ans 15 ans 13 ans 15 ans 14 ans 14 ans 13 ans 15 ans 16 ans 12 ans 15 ans 13 ans 16 ans 14 ans 15 ans

1.1 Indiquer le nombre total d’adolescents inscrits cette semaine de vacances.

1.2 Sachant que la somme totale des âges des adolescents est de 284, calculer l’âge moyen des adolescents inscrits cette semaine.

1.3 Une partie des données est reportée dans le tableur ci-dessous. Compléter la colonne des effectifs.

1.4 Quelle formule faut-il saisir dans la cellule C3 du tableur de la page précédente pour calculer le pourcentage des adolescents ayant 13 ans ? Cocher la bonne réponse.

 = B3/B7*100

 = B3*B7*100

 = B3*B7/100

1.5 Compléter la colonne des fréquences du tableur de la page précédente.

1.6 Blandine, une animatrice, affirme que « plus de la moitié des adolescents ont moins de 15 ans ». Indiquer si Blandine a raison. Justifier la réponse.

Exercice 2 :

La première journée, trois sorties sont prévues. Les adolescents sont répartis à l’aide d’un tirage au

sort. Pour cela, les animateurs déposent les 20 papiers suivants dans un sac :

- 10 papiers notés « cinéma »,

- 4 papiers notés « centre aquatique »,

- 6 papiers notés « escape game ».

Chaque adolescent tire un papier au hasard pour connaître son activité.

2.1 Thomas est le premier à tirer au hasard un papier dans le sac. Quelle est la probabilité que Thomas aille au centre aquatique ? Cocher la bonne réponse.

2.2 Calculer la probabilité que Thomas aille au cinéma.

Quand arrive le tour de Clémence, il ne reste plus que 5 papiers :

- 2 « escape game »,

- 2 « cinéma »,

- 1 « centre aquatique ».

Clémence est déçue, car il ne reste plus qu’un papier pour aller au centre aquatique.

2.3 Calculer la probabilité que l’activité de Clémence soit le centre aquatique.

2.4 Thomas dit à Clémence qu’elle a autant de chance que lui d’obtenir le centre aquatique.

Indiquer s’il a raison. Justifier la réponse.

Exercice 3 :

Pour préparer cette sortie, Blandine, l’animatrice, a consulté les différents tarifs du centre aquatique. Voici les deux tarifs possibles :

Tarif 1 : Forfait journée à 30 € par personne Tarif 2 : 5 € par heure et par personne dans le centre aquatique 3.1 Calculer, en euro, le prix à payer par personne, avec le tarif 2 pour 3 heures dans le centre aquatique.

3.2 En payant 10 € avec le tarif 2, calculer en heure, le temps passé au centre aquatique.

3.3 Compléter le tableau suivant pour le tarif 2 :

3.4 Placer les points B et C définis à la question précédente dans le repère suivant

3.5 Tracer la droite qui passe par les points A, B, C et D.

3.6 Clémence et Thomas souhaitent rester de 10h00 à 15h00 dans le centre aquatique. Indiquer le tarif le plus intéressant. Justifier la réponse.

<<<CORRECTION>>>

Sujet corrigé de Mathématique CAP production d’énergie électrique

En 2019, en France, la production d’énergie électrique s’élevait à 537,7 TWh (Térawattheure). Cette énergie provient de sources d’énergie non renouvelables (nucléaire, gaz, etc.) et renouvelables (éolien, solaire, etc.). La répartition des sources d’énergie est présentée dans le diagramme ci-contre.

<<<CORRECTION>>>

Exercice 1 : les différentes sources d’énergie renouvelables

Luc, élève en première année de CAP, souhaite réaliser un exposé sur les énergies renouvelables. Pour cela, il veut représenter graphiquement la répartition de ces énergies.

1.1. Calculer, en pourcentage, la part des énergies renouvelables dans la production électrique française.

1.2. Calculer, en TWh, la quantité d’énergie produite par les énergies renouvelables. Arrondir le résultat au dixième.

1.3. Luc a obtenu, après plusieurs recherches, la production (en TWh) des différentes sources d’énergie :

1.3.1. Déterminer les fréquences correspondant à l’énergie solaire et à la bioénergie. Arrondir

les résultats au dixième.

Indiquer les calculs :

1.3.2. Compléter la colonne des fréquences.

1.3.3. Calculer les angles correspondant à l’énergie solaire et à la bioénergie. Arrondir le

résultat à l’unité. Indiquer les calculs.

1.3.4. Compléter la colonne des angles.

1.4. Citer le type de diagramme que Luc va pouvoir utiliser pour représenter ses résultats.

Répondre par une phrase.

1.5. Construire ce diagramme en faisant apparaître la légende.

Exercice 2 : installation des panneaux photovoltaïques sur le toit

Les parents de Luc décident d’équiper leur toit avec des panneaux solaires. Ils doivent choisir le nombre de panneaux à installer. Un vendeur leur fournit cette documentation qui donne quelques exemples :

Le toit de la maison a une surface de 48 m². De ce fait, les parents de Luc se demandent quelle est la puissance d’installation maximale qu’ils pourront avoir, ainsi que le nombre de panneaux.

2.1. Préciser pourquoi on ne peut pas indiquer, par une lecture directe du Tableau 1, la puissance maximale et le nombre de panneaux pour un toit de surface 48 m² .

2.2. Proposer une démarche mathématique pour déterminer la puissance maximale. Ne pas rédiger ici le calcul.

On a représenté à partir des données du tableau 1, à l’aide d’un logiciel, la puissance d’installation (en kW) en fonction de la surface nécessaire (en m² ).

2.4. Cocher la fonction qui modélise la situation :

 Fonction affine

 Fonction linéaire

2.5. À l’aide du graphique précédent, déterminer la puissance d’installation correspondant à une surface de 48 m². Laisser apparents les traits utiles à la lecture.

…………………………………………………………………………………………………………

2.6. Sachant que la puissance est proportionnelle au nombre de panneaux, calculer le nombre de panneaux nécessaires pour une puissance de 10 kW. Arrondir le résultat à l’unité supérieure.

Exercice 3 : installation d’un panneau photovoltaïque sur un mur

Les parents de Luc décident de rajouter un panneau solaire sur un mur exposé au sud. Pour cela, il leur faut acheter un support mural.

Ce support est constitué de deux équerres et de deux traverses métalliques sur lesquelles sera posé le panneau solaire.

Le panneau solaire a une largeur de 1 m. Les parents se demandent si le support est adapté.

3.1. Une équerre peut être modélisée par un triangle ABC rectangle en B (représenté sur la figure ci-dessus). Sélectionner le côté du triangle sur lequel sera posé le panneau solaire.

 Le côté AB

 Le côté AC

 Le côté BC

3.2. Cocher le nom de ce côté sur lequel sera posé le panneau solaire.

 Côté de l’angle droit

 Rayon

 Hypoténuse

3.1. Une équerre peut être modélisée par un triangle ABC rectangle en B (représenté sur la figure ci-dessus). Sélectionner le côté du triangle sur lequel sera posé le panneau solaire.

 Théorème de Thalès

 Théorème de Pythagore

 Trigonométrie

3.3. Parmi les méthodes proposées, cocher celle qui permet de calculer la longueur du côté sélectionné à la question

3.4. Calculer la longueur du côté sélectionné. Arrondir le résultat au dixième. Rédiger la réponse.

3.5. Indiquer si le support est adapté. Justifier la réponse

<<<CORRECTION>>>

Mathématiques CONCOURS EXTERNE D’ADJOINT ADMINISTRATIF PRINCIPAL DE 2e CLASSE Épreuve écrite d'admissibilité n°2

Épreuve écrite consistant en courts exercices destinés à évaluer les capacités du candidat en français (vocabulaire, orthographe, grammaire) et mathématiques.

Durée: 1h30 (2 heures pour les candidats ayant un tiers temps) Coefficient : 3

Agent de maîtrise - Concours externe Épreuve écrite - Résolution de problèmes mathématiques

ADJOINT TECHNIQUE TERRITORIAL PRINCIPAL DE 2ème CLASSE EXAMEN PROFESSIONNEL AU TITRE DE L'AVANCEMENT DE GRADE

--------------------------------------------------------------------
Sujets du concours d'adjoint technique territorial
---------------------------------------------------------------------

SPÉCIALITÉ "ENVIRONNEMENT, HYGIÈNE"

LE NETTOYAGE D'UNE SALLE

Vous êtes adjoint technique territorial principal de 2ème classe, en charge du ménage au sein d’une collectivité. Vous devez, une fois par semaine, nettoyer le sol et les vitres de la salle du conseil municipal ainsi que le local de rangement.

Voici le plan représentant les différentes surfaces :

QUESTION 1 : CALCUL DE SURFACES ET VOLUMES (détailler les calculs)

1. Calculez les surfaces au sol pour chaque salle ainsi que la surface totale de ces deux salles (2 points) - Salle du conseil municipal :

............................................................................................................................................................

Local de rangement :

............................................................................................................................................................

- Surface totale :

............................................................................................................................................................

2. La salle comprend 3 baies vitrées de 2m de long et de 2m de haut. Calculez la surface totale de vitres à nettoyer (1 point)

............................................................................................................................................................

3. Vous répondrez à l'aide de l'annexe n°1. Le produit pour le sol est dosé à 0,5% pour 5 litres d’eau et vous utilisez un seau de 10 litres chaque semaine pour ces salles.

Calculez le volume en litres de produit à utiliser par an pour nettoyer le sol de ces deux salles, ainsi que le nombre de bidon(s) à prévoir à l’année (2 points)

............................................................................................................................................................

4. Le nettoyage de la totalité de la salle du conseil est réalisé en 20 minutes. Partant du constat que la cadence de travail est identique, combien de temps mettrez-vous pour nettoyer les vitres ? (2 points) .

............................................................................................................................................................

À l'aide de l'annexe n°2, préciser quel temps de pose il faut respecter afin que le produit pour les vitres ait une action bactéricide efficace (1 point)

............................................................................................................................................................

QUESTION 2 : PICTOGRAMMES

À l’aide de vos connaissances, renseignez la signification et les caractéristiques de ces pictogrammes (2 points)

2ème PARTIE : LA GESTION DES DÉCHETS (10 POINTS)

QUESTION 1 : LE TRI DES DÉCHETS
Dans le cadre de vos missions d’adjoint technique en charge du ménage de la mairie de X, vous êtes en
charge du tri des déchets. Les élus sont sensibilisés et veulent que la mairie soit vertueuse en maximisant le tri des déchets. Dans la salle du conseil que vous venez de nettoyer, vous trouvez une série de déchets qu’il faut débarrasser.
À l'aide des annexes n°3 et n°4, indiquez, dans le tableau ci-dessous, si les déchets listés peuvent être triés et, si oui, dans quel(s) contenant ou destination. Vous préciserez également le devenir de chaque objet.

Les cases grisées ne doivent pas être complétées.

Liste de déchets présents dans la salle du conseil (3 points)

QUESTION 2 : LES EPI ET LA PRÉVENTION

1. Définir ce qu’est un EPI. Quel est son rôle ? (1 point)

2. À l'aide de vos connaissances personnelles et de l'annexe n°5, répondez à la question suivante :
qu’est-ce que la prévention ? Après avoir défini la notion, citer un outil et un acteur de la prévention (2 points)

3. À l'aide des annexes n°5 et n°6, lister les principaux risques liés au métier d’agent de collecte des
déchets, ainsi que les EPI associés (4 points)

--------------------------------------------------------------------
Sujets du concours d'adjoint technique territorial
---------------------------------------------------------------------

Problème de mathématique CAP

CERTIFICAT D'APTITUDE PROFESSIONNELLE

PRODUCTIQUE - MAINTENANCE - BÂTIMENT - TRAVAUX PUBLICS - ELECTRICITE - ELECTRONIQUE - AUDIOVISUEL - INDUSTRIES GRAPHIQUES

Des radars qui vous veulent du bien.

Un radar pédagogique est un radar automatique qui affiche la vitesse des automobilistes passant dans une zone débutant à 200 mètres environ avant le panneau afficheur.

Il est sans but répressif mais dans un objectif d’information et de prévention.

Exercice 1 :

Achat d’un radar pédagogique. Une mairie veut s'équiper d’un radar pédagogique. Elle sélectionne sur un site internet l’offre suivante :

Description générale du radar :

RADLed – Solaire : Radar Afficheur de Vitesse à LEDs. Alimenté par son panneau solaire le jour et une batterie permettant son fonctionnement de nuit.

Prix d’achat brut hors taxe : 2470,00 €

Options :

- Bicolore : LEDs rouges et vertes : + 170,00 € hors taxe.

- Pack statistiques : + 310,00 € hors taxe.

Pour fidéliser sa clientèle, l’entreprise accorde à la mairie une remise de 147,50 € sur le prix d’achat brut hors taxe avec options.

1.1. Compléter le tableau suivant en utilisant les informations de l’offre :

1.1.1. Détailler ci-dessous les calculs suivants :

- Taxe sur la valeur ajoutée =

- Prix de vente taxe comprise =

1.1.2. Calculer le pourcentage de la remise accordée à la mairie. Donner le détail du calcul. Arrondir à l’unité.

1.2. Indiquer si un budget de 3500,00 € est suffisant pour l’achat d’un radar pédagogique avec les deux options et en tenant compte de la remise. Justifier et rédiger une phrase.

Exercice 2 :

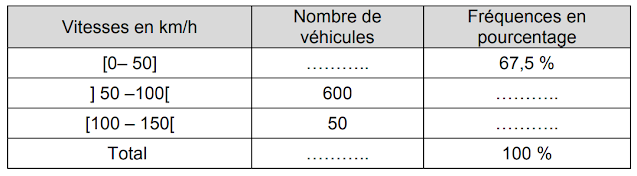
Exploitation des données statistiques du radar pédagogique. Le logiciel fourni avec le radar équipé de l’option « Pack statistiques » donne accès à l’exploitation des données du trafic. Voici les statistiques fournies par le logiciel sous forme de tableau récapitulatif des vitesses pratiquées par 2000 véhicules sur une portion de voie limitée à 50 km/h:

2.1. Calculer le nombre de véhicules qui ont respecté la vitesse autorisée. En déduire le nombre de ceux qui ne l’ont pas respectée.

2.2. Calculer les pourcentages manquants dans la colonne « Fréquences en pourcentage ».

2.3. Compléter le tableau statistique.

2.4. Cocher la bonne réponse : Le pourcentage des automobilistes qui n’ont pas respecté la limitation de vitesse est de :

30 %
32,5 %
67,5 %

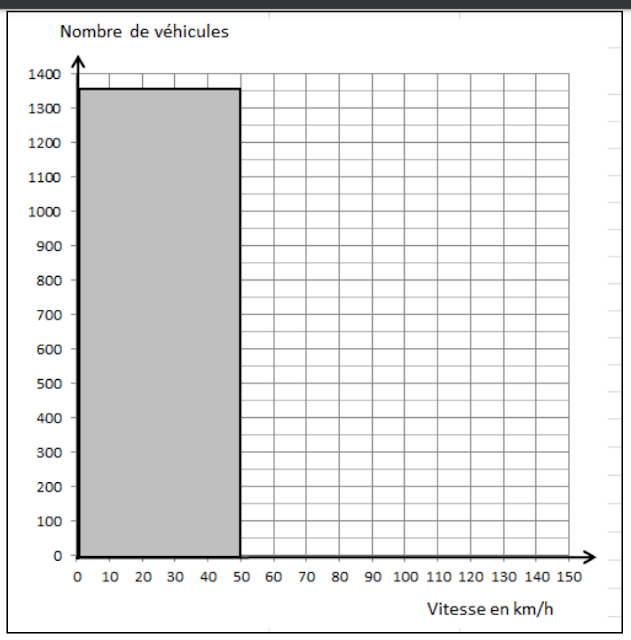
2.5. À partir du tableau statistique, compléter le diagramme ci-dessous.

Répartition des vitesses pratiquées par 2000 véhicules sur une portion de voie limitée à 50 km/h.

Exercice 3 :

Installation du radar. Pour un rendement maximal, le panneau solaire doit être exposé plein-sud et incliné de 30 degrés au point B conformément à la figure ci-dessous.

3.1. Nous savons que le triangle ABC est rectangle en A, le segment [BC] mesure 50 cm et l’angle est égal à 30°. On propose de représenter l’installation du radar par le schéma ci-après :

3.1.1. Cocher la bonne réponse.

Le segment [AC] est :

l’hypoténuse
le côté opposé à l’angle
le côté adjacent à l’angle B

3.1.2. En utilisant l’une des relations dans le triangle rectangle du formulaire page 21/21, calculer en cm, la longueur du segment [AC]. Arrondir à l’unité.

3.2. En déduire la longueur du segment [AC] pour avoir un rendement maximal du panneau solaire. Rédiger une phrase.

Problème de mathématique CAP Employé de commerce multi-spécialités

Les élèves de la classe de cette section souhaitent organiser une sortie au cinéma.

Pour financer cette sortie, ils décident avec l’un de leur professeur de réaliser des gaufres et de les vendre à la récréation. Ils prévoient de vendre une gaufre à chaque élève des 4 classes de CAP.

Il y a 20 élèves dans chaque classe

Les élèves pensent démarrer la cuisson des gaufres à 8h30 pour les servir à la récréation de 10h. Le but de l’exercice est de déterminer si les élèves auront suffisamment de lait et le temps nécessaire pour réaliser toutes les gaufres.

Calculer le nombre total de gaufres que la classe prévoit de préparer.

Compléter le tableau ci-dessous.

2.3 Deux bouteilles de 1 litre de lait ont été achetées. Indiquer si ces deux bouteilles suffiront pour réaliser 80 gaufres. Justifier la réponse.

Les élèves ne disposent que d’un seul gaufrier. Le temps de cuisson de 2 gaufres est de 3 min. Vérifier que la durée de cuisson nécessaire pour cuire 80 gaufres est 120 min. Justifier la réponse.

En déduire si les élèves auront suffisamment de temps pour cuire toutes les gaufres avant la récréation en commençant à 8 h 30. Justifier la réponse.

Calculer l’heure à laquelle les élèves devraient commencer la cuisson des gaufres afin qu’elles soient toutes cuites à la récréation de 10h. Justifier la réponse.

Exercice de mathématique Dans la section CAP Préparation et réalisation d'ouvrages électriques

Un élève doit mesurer la valeur de différentes résistances (conducteurs ohmiques) à sa disposition. Les résultats obtenus sont représentés ci-dessous sous la forme d’un histogramme.

Le but de cet exercice est de vérifier l’affirmation de l’élève : « plus de 55 % des résistances mesurées ont une valeur supérieure ou égale à 120 ohms »

1.1 Indiquer le caractère étudié par l’élève lors de cette étude.

1.2 Préciser la nature de ce caractère : qualitatif ou quantitatif. Justifier la réponse.

1.3 Parmi les démarches suivantes, cocher celle qui permet de calculer le pourcentage de résistances qui ont une valeur supérieure ou égale à 120 ohms.

Démarche n°1

Je calcule le nombre total de résistances. Je divise le nombre total de résistances par 6. Je multiplie le résultat précédent par 100.

Démarche n°2

Je calcule le nombre total de résistances. Je calcule le nombre de résistances qui ont une valeur supérieure ou égale à 120 ohms. Je divise le nombre de résistances qui ont une valeur supérieure ou égale à 120 ohms par le nombre total de résistances. Je multiplie le résultat précédent par 100.

Démarche n°3

Je calcule le nombre total de résistances. Je calcule le nombre de résistances qui ont une valeur supérieure ou égale à 120 ohms. Je multiplie le nombre total de résistances par le nombre de résistances qui ont une valeur supérieure ou égale à 120 ohms.

1.4 Le professeur propose à l’élève une autre démarche pour répondre à la problématique. Il a regroupé les résultats dans le tableau incomplet ci-dessous. Calculer les fréquences en pourcentage manquantes et compléter la 3e colonne du tableau. Arrondir au dixième. Détailler l’un des deux calculs réalisés.

1.5 Indiquer si l’affirmation : « plus de 55 % des résistances mesurées ont une valeur supérieure ou égale à 120 ohms » est correcte ? Justifier la réponse.

Problèmes de mathématique niveau CAP, BEP

CERTIFICAT D'APTITUDE PROFESSIONNELLE - PRODUCTIQUE – MAINTENANCE – BÂTIMENT – TRAVAUX PUBLICS – ÉLECTRICITÉ – ÉLECTRONIQUE – AUDIOVISUEL – INDUSTRIES GRAPHIQUES

Face à une concurrence étrangère de plus en plus forte dans l’industrie textile, Monsieur PALTOT, directeur d’une entreprise française de confection de vêtements, décide d’analyser les différents postes de sa chaîne de production en vue d’améliorer sa compétitivité.

Exercice 1 :

Monsieur PALTOT doit confectionner des jupes pour une chaine de magasin. Il s’intéresse tout d’abord au temps mis par ses 20 couturières pour fabriquer une jupe. Les durées sont regroupées dans le tableau suivant :

1.1. Compléter la colonne des « effectifs » du tableau statistique précédent.

1.2. Calculer le nombre de couturières confectionnant une jupe en moins de 36 minutes.

1.3. Compléter la colonne des « fréquences » du tableau statistique.

1.4. Calculer le pourcentage de couturières mettant moins de 36 minutes pour fabriquer une jupe. Justifier votre calcul.

1.5. A partir du tableau statistique, compléter l’histogramme ci-dessous.

Exercice 2 : Matériel nécessaire

Monsieur PALTOT se rend chez son grossiste et choisit le matériel nécessaire pour confectionner 100 jupes.

2.1. Le matériel nécessaire pour la confection de 100 jupes, est indiqué dans le tableau ci-dessous. Compléter le nombre de sachets de 10 boutons nécessaire pour confectionner les 100 jupes sachant qu’il faut 100 boutons.

2.2. Compléter la colonne « Montant » du tableau.

2.3. Sachant que Monsieur PALTOT dispose de 400 €, indiquer si son budget est suffisant pour acheter tout le matériel nécessaire pour confectionner les 100 jupes. Justifier votre réponse.

Exercice 3 : Confection

Le modèle de la jupe (appelé patron) que les couturières doivent confectionner est donné ci-dessous : (Attention le modèle n’est pas à l’échelle)

3.1. Nommer la figure géométrique ABCD composant une partie de la jupe sachant que AB = CD, BC = AD et ABC=90°

3.2. Calculer l’aire du quadrilatère ABCD. On donne l’aire d’un rectangle : où est la longueur et est la largeur

3.3. Sachant que l’aire du quadrilatère DCEF est de 4050 cm², calculer l’aire totale de tissu nécessaire pour confectionner une face de la jupe.

La face de la jupe est découpée à partir d’un morceau de tissu rectangulaire de longueur 120 cm et de largeur 80 cm.

3.4. Calculer l’aire de ce morceau de tissu rectangulaire.

3.5. A partir du résultat de la question 3.4, calculer l’aire de tissu perdu.

3.6. Donner le pourcentage de perte du tissu (arrondir le résultat à l’unité). Une bande de ruban doit être cousue sur le côté de la jupe.

3.7.1. Quelle propriété peut-être utilisée pour calculer la longueur du ruban CE ? Justifier votre réponse.

 Propriété de Pythagore

 Propriété de Thalès

3.7.2. Calculer cette longueur CE. Arrondir à la dizaine de centimètres supérieure.

Pages

Rechercher dans ce blog

Exercices de mathématique pour préparer le CAP cuisine

Problèmes et exercices de mathématique niveau CAP

CAP épreuve de mathématiques tertiaires, services, hôtellerie, alimentation, restauration

Sujet corrigé de Mathématique CAP production d’énergie électrique

Mathématiques CONCOURS EXTERNE D’ADJOINT ADMINISTRATIF PRINCIPAL DE 2e CLASSE Épreuve écrite d'admissibilité n°2

Agent de maîtrise - Concours externe Épreuve écrite - Résolution de problèmes mathématiques

ADJOINT TECHNIQUE TERRITORIAL PRINCIPAL DE 2ème CLASSE EXAMEN PROFESSIONNEL AU TITRE DE L'AVANCEMENT DE GRADE

Problème de mathématique CAP

Problème de mathématique CAP Employé de commerce multi-spécialités

Exercice de mathématique Dans la section CAP Préparation et réalisation d'ouvrages électriques

Problèmes de mathématique niveau CAP, BEP

Sujets corrigés des concours à télécharger en pdf!