CERTIFICAT D'APTITUDE PROFESSIONNELLE
PRODUCTIQUE - MAINTENANCE - BÂTIMENT - TRAVAUX PUBLICS - ELECTRICITE - ELECTRONIQUE - AUDIOVISUEL - INDUSTRIES GRAPHIQUES
Des radars qui vous veulent du bien.
Un radar pédagogique est un radar automatique qui affiche la vitesse des automobilistes passant dans une zone débutant à 200 mètres environ avant le panneau afficheur.
Il est sans but répressif mais dans un objectif d’information et de prévention.
Exercice 1 :
Achat d’un radar pédagogique. Une mairie veut s'équiper d’un radar pédagogique. Elle sélectionne sur un site internet l’offre suivante :
Description générale du radar :
RADLed – Solaire : Radar Afficheur de Vitesse à LEDs. Alimenté par son panneau solaire le jour et une batterie permettant son fonctionnement de nuit.
Prix d’achat brut hors taxe : 2470,00 €
Options :
- Bicolore : LEDs rouges et vertes : + 170,00 € hors taxe.
- Pack statistiques : + 310,00 € hors taxe.
Pour fidéliser sa clientèle, l’entreprise accorde à la mairie une remise de 147,50 € sur le prix d’achat brut hors taxe avec options.
1.1. Compléter le tableau suivant en utilisant les informations de l’offre :
1.1.1. Détailler ci-dessous les calculs suivants :
- Taxe sur la valeur ajoutée =
- Prix de vente taxe comprise =
1.1.2. Calculer le pourcentage de la remise accordée à la mairie. Donner le détail du calcul. Arrondir à l’unité.
-
-
-
-
1.2. Indiquer si un budget de 3500,00 € est suffisant pour l’achat d’un radar pédagogique avec les deux options et en tenant compte de la remise. Justifier et rédiger une phrase.
-
-
-
-
Exercice 2 :
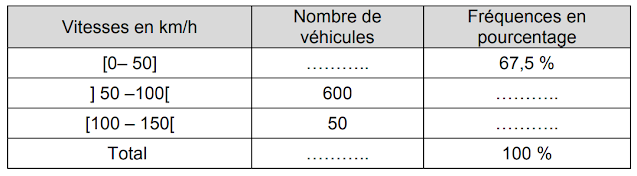
Exploitation des données statistiques du radar pédagogique. Le logiciel fourni avec le radar équipé de l’option « Pack statistiques » donne accès à l’exploitation des données du trafic. Voici les statistiques fournies par le logiciel sous forme de tableau récapitulatif des vitesses pratiquées par 2000 véhicules sur une portion de voie limitée à 50 km/h:
2.1. Calculer le nombre de véhicules qui ont respecté la vitesse autorisée. En déduire le nombre de ceux qui ne l’ont pas respectée.
2.2. Calculer les pourcentages manquants dans la colonne « Fréquences en pourcentage ».
2.3. Compléter le tableau statistique.
2.4. Cocher la bonne réponse : Le pourcentage des automobilistes qui n’ont pas respecté la limitation de vitesse est de :
- 30 %
- 32,5 %
- 67,5 %
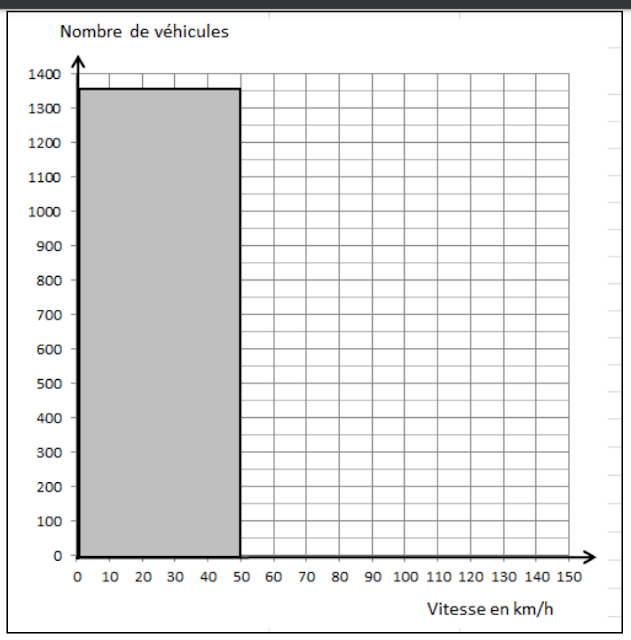
2.5. À partir du tableau statistique, compléter le diagramme ci-dessous.
3.1. Nous savons que le triangle ABC est rectangle en A, le segment [BC] mesure 50 cm et l’angle est égal à 30°. On propose de représenter l’installation du radar par le schéma ci-après :
3.1.1. Cocher la bonne réponse.
Le segment [AC] est :
- l’hypoténuse
- le côté opposé à l’angle
- le côté adjacent à l’angle B
3.1.2. En utilisant l’une des relations dans le triangle rectangle du formulaire page 21/21, calculer en cm, la longueur du segment [AC]. Arrondir à l’unité.
-
-
-
-
3.2. En déduire la longueur du segment [AC] pour avoir un rendement maximal du panneau solaire. Rédiger une phrase.
-
-
-
-